[그래프 이론] 그래프 정의 및 성질

그래프의 역사

그래프 이론은 저명한 수학자 레온하르트 오일러(Leonhard Euler)에 의해 고안되었습니다. 오일러는 '쾨니히스베르크의 다리 문제'를 해결하기 위해 처음으로 그래프 이론을 사용했다고 합니다. 쾨니히스베르크의 다리 문제는 다음과 같습니다.

 

사진출처: 위키피디아

 

당시 쾨니히스베르크에는 7개의 다리가 있었습니다. 모든 다리를 한 번씩만 건너서 처음 출발했던 장소로 되돌아 오는 게 가능한지에 대한 문제가 '쾨니히스베르크의 다리 문제' 입니다. 오일러는 이 문제를 해결하면서 그래프의 개념을 도입했습니다.

 

위 문제의 답은 불가능하다입니다. 각 정점에서 들어오는 간선과 나가는 간선의 수가 동일해야 , 즉 모든 정점의 차수가 짝수여야 처음 출발했던 정점으로 되돌아 올 수 있습니다.

 

 

그래프 정의 및 성질

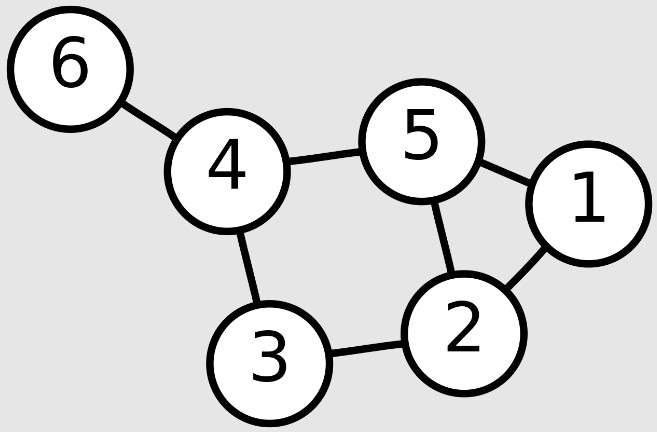
사진출처: 위키피디아

 

그래프(Graph)는 정점(vertex)의 집합과 간선(모서리, 영어: edge)집합으로 구성됩니다. 정점(vertex)은 위 사진에서 숫자 6, 4, 3에 해당하는 것처럼 연결의 대상이 되는 개체 또는 위치를 의미하고, 간선(edge)은 이들 정점 사이를 연결하는 선입니다. 그래프를 \(G=(V, E) \)로 표시합니다. 정점과 간선의 개수는 각각 \(\left| V\right|\), \(\left| E\right|\)로 표시합니다.

 

\(V\): 정점(vertex 또는 node)의 집합
\(E\): 간선(모서리, 영어: edge)의 집합

 

위 그래프를 집합으로 표현하면 다음과 같습니다.

$$
\begin{align*}
& V = \left\{6, 4, 5, 1, 2, 3 \right\} \\
& E = \left\{\left\{6, 4 \right\}, \left\{4, 5 \right\}, \left\{5, 1 \right\}, \left\{1, 2 \right\}, \left\{2, 5 \right\}, \left\{3, 2 \right\}, \left\{3, 4 \right\} \right\}
\end{align*}
$$

 

무방향 그래프(Undirected graph)의 종류

사진출처: researchgate.net

• 단순 그래프(Simple graph): 정점과 정점이 하나의 간선으로 연결되어 있거나 연결되어 있지 않은 그래프입니다.
• 멀티그래프(Multigraph): 두 정점 사이에 여러 개의 간선이 존재할 수 있는 그래프입니다.

사진출처: 위키미디어

특히 자기 자신과 자기 자신을 연결하는 간선을 루프(loop)이라고 부릅니다. 단순 그래프는 루프(loop)가 없습니다.

 

 

방향 그래프(Directed graph)의 종류

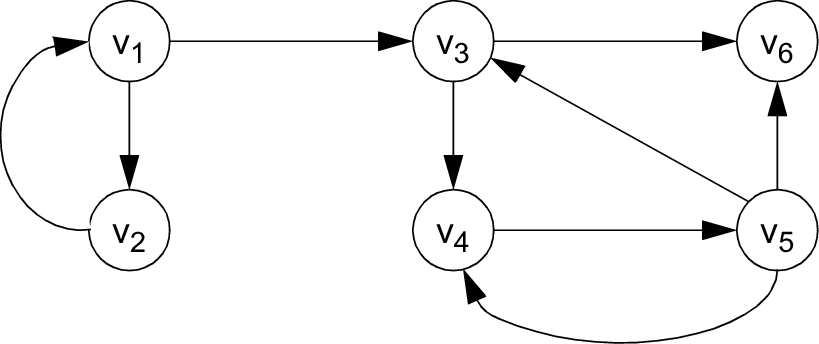
사진출처: researchgate.net

• 방향 그래프(Directed graph): 간선에 방향정보가 포함된 그래프를 가리켜 방향 그래프라고 합니다.
• 방향 멀티그래프(Directed multigraph): 두 정점 사이에 여러 개의 방향 간선이 존재할 수 있는 그래프입니다.

방향 그래프에서 정점 \(V_1\)과 정점 \(V_3\)를 연결하는 간선을 (\(V_1\) , \(V_3\))으로 표시합니다. 간선 (\(V_1\) , \(V_3\)) 는 정점 \(V_1\)에서 \(V_3\)으로의 방향성을 가집니다. (\(V_1\) , \(V_3\))을 \(V_1\)으로부터 \(V_3\)으로의 방향 간선(arc 또는 directed edge)라고 부릅니다. (소괄호는 보통 순서쌍을 표현한다는 의미)

• 정점 \(V_1\)은 (\(V_1\) , \(V_3\))의 시작점(initial vertext)라고 한다.
• 정점 \(V_3\)은 (\(V_1\) , \(V_3\))의 끝점(terminal vertex)라고 한다.

 

완전 그래프(Complete graph)

사진출처: mathworld.wolfram.com

무방향 그래프와 방향 그래프는 간선의 연결형태에 따라서 완전 그래프(complete graph)로 구분됩니다. 완전 그래프는 각각의 모든 정점들이 다른 모든 정점들과 연결된 그래프를 말합니다. 정점이 \(n\)개 있는 그래프를 \(k_n\)이라 표시하고 \(k_n\)의 간선의 개수는 \(\begin{pmatrix}n \\2\end{pmatrix}\) 입니다. 

 

부분 그래프(Sub graph)

사진출처: 위키피디아

부분 집합과 유사한 개념으로 부분 그래프라는 것이 있습니다. 그래프 G의 부분 그래프는 G의 정점과 간선 일부로 구성된 그래프입니다.

 

가중치 그래프(Weight graph)

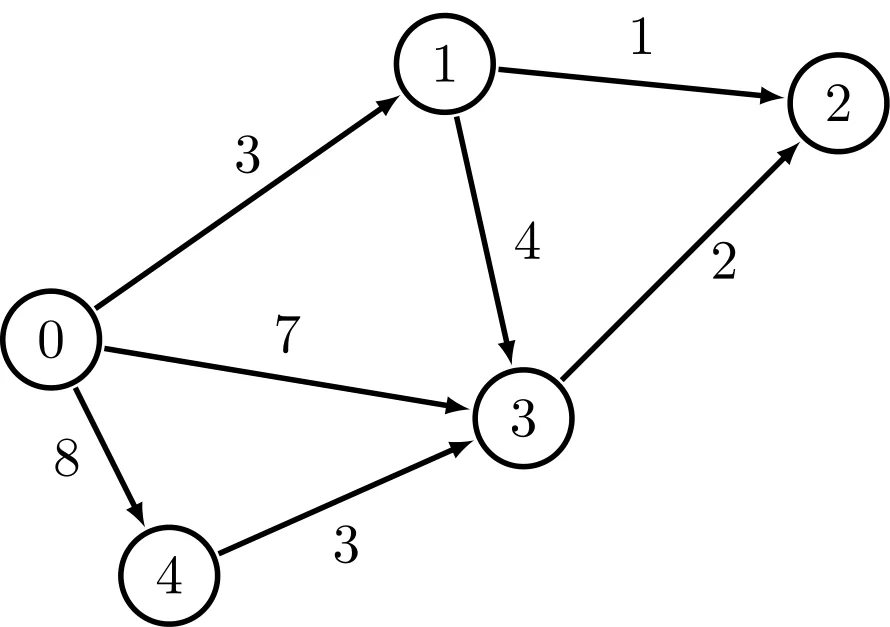
사진출처: hyperskill.org

위 그래프처럼 간선에 어떤 정보를 부여할 수 있다. 저 정보는 두 정점 사이의 거리라던가 두 정점을 이동하는 데 걸리는 비용과 같은 정보가 될 수 있다. 이러한 정보를 가중치라고 부르고 간선에 가중치가 부여된 그래프를 가중치 그래프라고 합니다.

 

인접(adjacent), 이웃(neighbor)

두 정점 \(u\)와 \(v\)가 간선(모서리)으로 연결되어 있으면 정점 \(u\)와 정점 \(v\)는 인접(adjacent) 또는 이웃(neighbors)한다고 합니다. 기호로는 \(u \sim v \) 이렇게 표시합니다. 또한, 정점 \(v\)의 모든 이웃들의 집합을 \(N(v)\)라 표시하고. 정점 \(v\)의 이웃(neighbors)이라고 부릅니다.

• \(u\)와 \(v\)가 서로 이웃: \(u \sim v \)
• \(v\)의 모든 이웃들의 집합: \(N(v)\)

 

차수(Degree)

사진출처: 위키피디아

 

정점 \(v\)의 차수는 정점 \(v\)에 붙어있는 간선들의 개수입니다. \(deg(v)\) 또는 \(d(v)\)로 표시합니다. 루프 간선은 정점 차수에 2번 가산합니다. 예를 들어 아래 그래프에서 \(deg(2) = 3\)이고 \(deg(1) = 4\) 입니다.

 

 

사진출처: 위키피디아

 

• 정점 \(v\)의 출력차수(out-degree) \(deg^+(v)\): 정점 \(v\)에서 나가는 간선의 수
• 정점 \(v\)의 입력차수(in-degree) \(deg^-(v)\): 정점 \(v\)으로 들어오는 간선의 수

$$
\begin{align*}
deg^+(3)=2 \\
deg^-(3)=2
\end{align*}
$$

 

악수 정리(Handshaking lemma)

그래프 𝐺=(𝑉,𝐸)에서 모든 정점의 차수(degree)의 합은 간선 수의 두배이다.

 

어떤 그래프 \(G=(V, E)\)가 \(m\)개의 간선을 갖는다고 할 때,

$$
\sum_{v\in V}^{} deg(v) = 2m
$$

임이 성립합니다.

모든 정점의 차수(degree)를 전부 더한 값과 간선의 개수(\(\left|E \right|\))에 2를 곱한 값은 같습니다.

 

 

사진출처: mymathangels

 

 

위 그래프에서 간선의 수는 \(m=8\). 그리고 각 정점의 차수는 다음과 같습니다.

 

$$
\begin{align*}
deg(a) = 4 \\
deg(b) = 7 \\
deg(c) = 3 \\
deg(d) = 2
\end{align*}
$$

 

따라서 다음과 같습니다.

$$
\begin{align*}
& \sum_{v\in V}^{} deg(v) = 2m \\
& = 4 + 7 + 3 + 2 = 2 \cdot 8 \\
& = 16
\end{align*}
$$

 

특히 위 식을 통해서 알 수 있는 건 모든 차수(degree)의 합이 짝수라는 사실입니다. 모든 수에 2를 곱하면 짝수가 되는데 우변에서 \(m\)에다가 2를 곱하여 \(2m\)이 되니 결국 좌변도 짝수가 됩니다.

 

또한 악수정리에 의해 다음과 같은 정리도 성립합니다.

그래프 𝐺=(𝑉,𝐸)에서 홀수 차수를 가지는 정점들은 짝수개 있다.

 

위 정리는 귀류볍을 사용하여 간단하게 증명할 수 있습니다. 홀수 차수를 가지는 정점이 홀수개 있다고 가정하고 위 정리와의 모순을 찾으면 됩니다.

 

\(V_1\): 짝수 차수를 가진 정점들의 집합

\(V_2\): 홀수 차수를 가진 정점들의 집합

 

$$
2m = \sum_{v\in V}^{} deg(v) = \sum_{v \in V_1}^{} deg(v) + \sum_{v \in V_2}^{} deg(v)
$$

시그마의 성질에 의해 각각의 시그마로 분리했습니다. 일단 짝수는 몇 번을 더해도 짝수이기 때문에  \( \sum_{v \in V_1}^{} deg(v) \)은 짝수가 됩니다. 하지만 \(V_2\)는 다릅니다. 만약  \(V_2\)의 원소가 홀수개 있다면 그 차수의 총합은 홀수가 됩니다. 그리고 홀수와 짝수를 더하면 홀수가 되므로 악수정리를 만족하지 못합니다. 즉, "홀수 차수를 가지는 정점이 홀수개 있다"라는 가정은 악수정리와 모순됩니다.

 

 

방향 그래프의 성질

$$
\sum_{v\in V}^{} deg^-(v) = \sum_{v\in V}^{} deg^+(v) = \left|A \right|
$$

 

방향성 그래프  \(D=(V, A)\)에서 모든 정점의 출력차수(out-degree)의 합과 입력차수(in-degree) 합 그리고 간선의 수는 서로 같습니다. 참가로 \(D\)의 의미는 Directed의 앞글자입니다. \(A\)는 Arc의 앞글자 입니다. 방향 간선은 arc라고도 부릅니다.